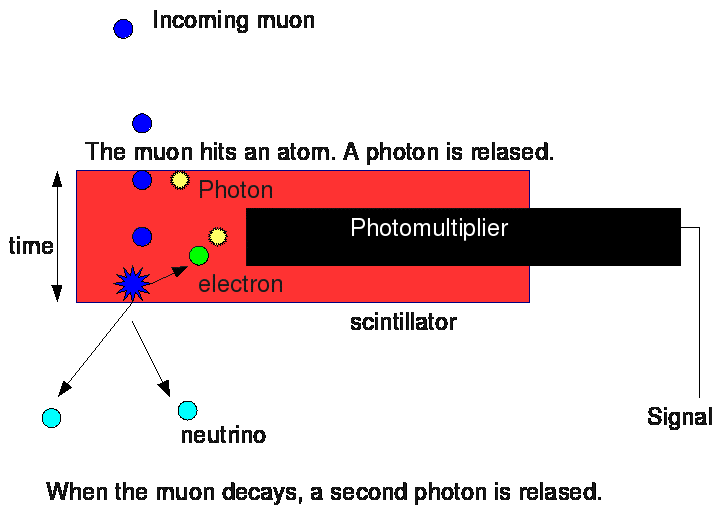
To measure the muon lifetime, we set up another experiment using scintillators. This time, we used three scintillators, a simple metal rectangular structure and some blocks of lead. We put the first scintillator on the top of the structure, the second inside it, on the lead blocks, and the third under it.

The idea was that the muons that go through the lead lose much of their energy (the lead is very dense) and stop in the third scintillator. Here they decay and we can measure the decay time (but most of the muons we detected seem to decay in the second scintillator).

Normally, muons have a very short lifetime (2.2 microseconds), after that they decay into an electron and two neutrinos. But, since they travel very fast and because of the time dilation, „their“ time goes much slower, and they can reach the ground before decaying. So, I already said that a muon entering the scintillator produces a photon. Well, in the decay process, energy is produced and so another atom is excited and emits another photon, still detected by the photomultiplier.

By calculating the time between these two signals, one can tell after how much time the muon has decayed. Since QuarkNet provides all the data it receives, in form of text lines, and since we care only of „double events“, Robert wrote a Python program that examines this data and takes only the „double events“, that is, an entering muon and a signal in one of the lower scintillators within 20 microseconds. The upper scintillator works as a veto for the decay signal (this means, events that

are not detected in the first scintillator and signals too far in time are considered as noise and ignorated. Muons that arrive while another muon is decaying are also ignorated).

In order to have a high amount of data (double events are rare), we let the scintillators run for 4 days, trying several positions and combinations of the material: after two days, we set the distance between the three scintillators much shorter and then we removed the lead. The quantity of data went much bigger and we were able to achieve a much more accurate lifetime measurement. This is because, with the detectors closer together, also muons that come from the side are detected, we have a wider angle.

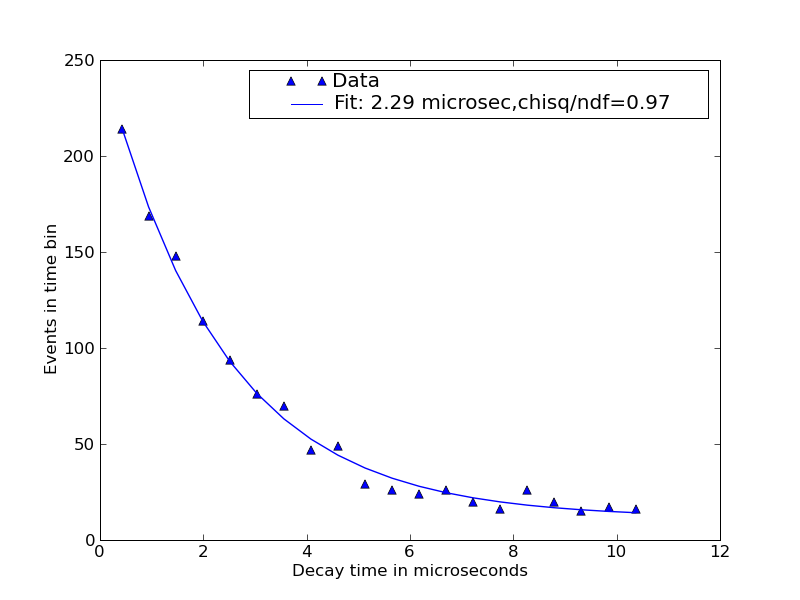
Using other programs, the theoretical lifetime curve was fit to the measurements to extract the lifetime.

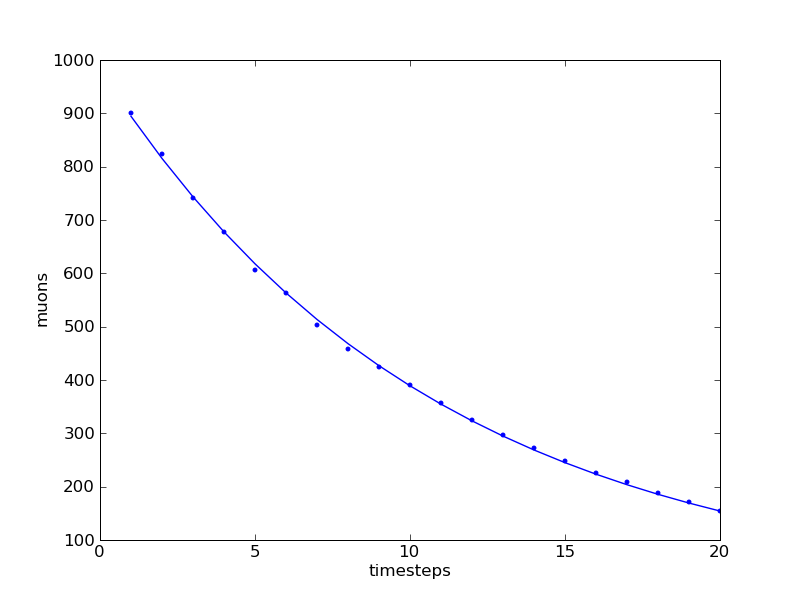
Then, after learning Python, a relatively simple programming language, I wrote another program to simulate muon decay, based on probability. The plot I took from the result was nearly matching the theoretical curve, because no experiment was done (also after all these precautions, there is a „noise“ probability).