Best sample texture viewer, V 1.0

by Florian Plentinger, Gerhart Seidl, Walter Winter

If you use the information from this notebook, please cite hep-ph/0612169

Installation instructions:
- Copy both QLCTextures.nb (Mathematica notebook) and samplenew.mmo (compressed best sample info) in a working directory
- Open QLCTexture.nb in Mathematica (developed for Version 5.2); make sure that it can find samplenew.mmo in the current directory
- Evaluate the Notebook with Kernel/Evaluation/Evaluate notebook
- Now you can use the Selector and PrintModel functions to extract subsamples from our best sample as you wish
NB: Only models from our best sample are included. Therefore, the selector will not find models absolutely incompatible with current data!

Some helper variables. We need this information to reconstruct the models from the compressed information:

In[1]:=

comblist = Flatten[Outer[List, Table[i, {i, 1, Length[allcombmat]}], Table[j, {j, 1, Length[allcombmatNU]}]], 1] ;

Helper functions needed to reconstruct  the different matrices. You will not need to use these functions directly.
All of the following take the expansion order εorder as parameter. if this parameter is >= 1, expand in ε, otherwise, use εorder as numerical value for ε.

In[3]:=

In[4]:=

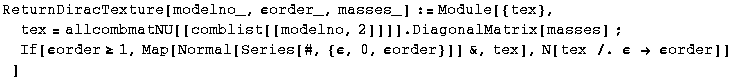
In[5]:=

In[6]:=

In[7]:=

Here we load our best sample. Make sure that it is in the current directory such that Mathematica can find it!

In[8]:=

bestsample = << "samplenew.mmo" ;

In[9]:=

bestsample = Sort[bestsample, (#1[[2, 1]] <#2[[2, 1]]) &] ;

The Selector function selects all models from the best sample with (all angles in degrees!)
theta12min<= θ_12<theta12max,  theta13min<= θ_13<theta13max, theta23min<= θ_23<theta23max,

In[10]:=

The PrintModels function prints a sample (list) of models , expanded up to order εorder, using the neutrino mass scheme masses. The list hierarchies illustrates three different choices for masses: normal hierarchy, inverse hierarchy, degenerate neutrinos

In[11]:=

hierarchies = {{ε^2, ε, 1}, {1, 1, ε}, {1, 1, 1}} ;

In[12]:=

Example: Assume that θ_13 is large. Choose all models with 30°<θ_12< 36°, 8°<θ_13< 9°, 44°<θ_23< 46° and print them with the analytical textures expanded up to second order in ε for a normal mass hierarchy:

In[13]:=

mysample = Selector[30, 36, 8, 9, 44, 46] ;

16 Models selected!

In[14]:=

PrintModels[mysample, 2, hierarchies[[1]]] ;

Chosen neutrino mass scheme: {ε^2, ε, 1}

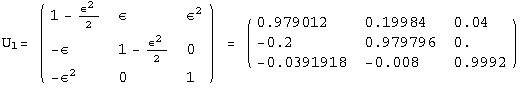
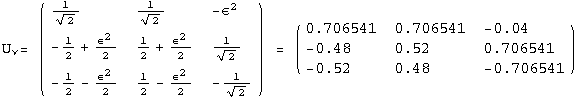
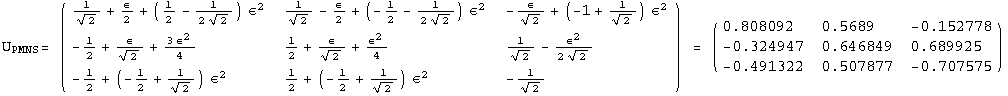
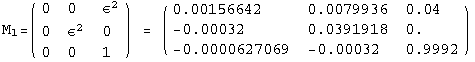
M = ( {{0, 0, ε^2}, {0, ε^2, 0}, {0, 0, 1}} ) = ( {{0.00156642, 0.0079936, 0.04}, {-0.00032, 0.0391918, 0.}, {-0.0000627069, -0.00032, 0.9992}} ) l

Chosen neutrino mass scheme: {ε^2, ε, 1}

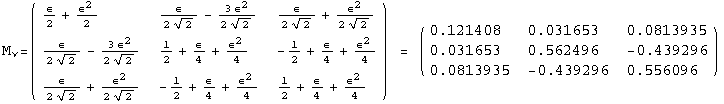
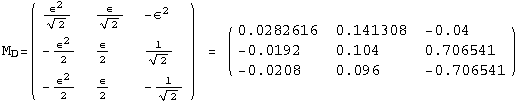
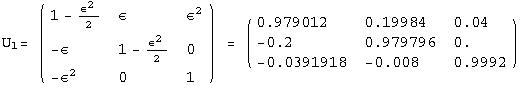
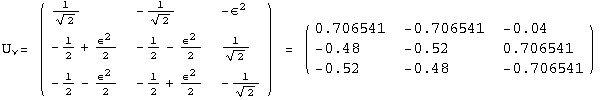
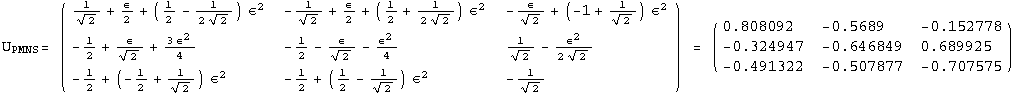
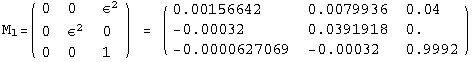
M = ( {{0, 0, ε^2}, {0, ε^2, 0}, {0, 0, 1}} ) = ( {{0.00156642, 0.0079936, 0.04}, {-0.00032, 0.0391918, 0.}, {-0.0000627069, -0.00032, 0.9992}} ) l

Chosen neutrino mass scheme: {ε^2, ε, 1}

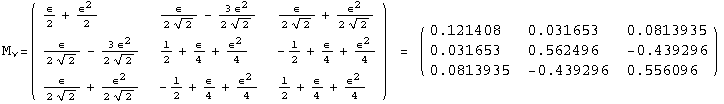
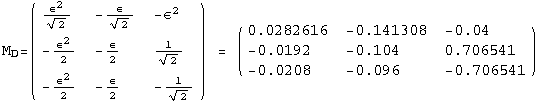
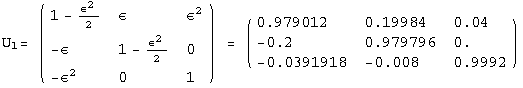
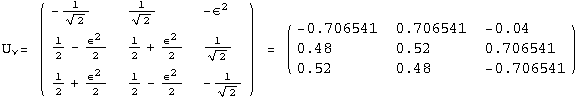
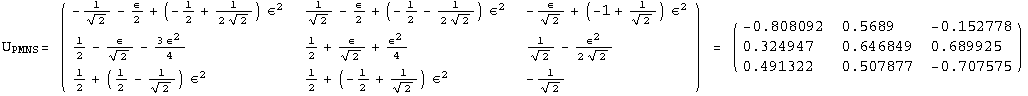
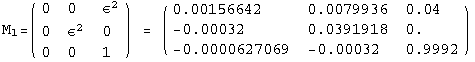
M = ( {{0, 0, ε^2}, {0, ε^2, 0}, {0, 0, 1}} ) = ( {{0.00156642, 0.0079936, 0.04}, {-0.00032, 0.0391918, 0.}, {-0.0000627069, -0.00032, 0.9992}} ) l

Chosen neutrino mass scheme: {ε^2, ε, 1}

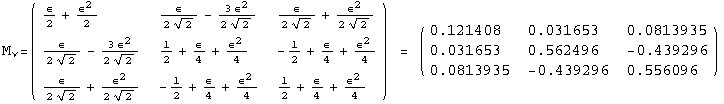
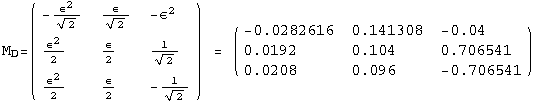
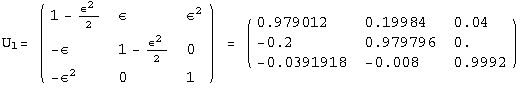
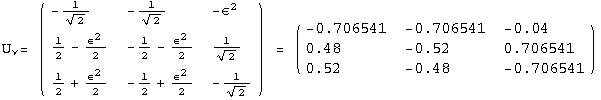
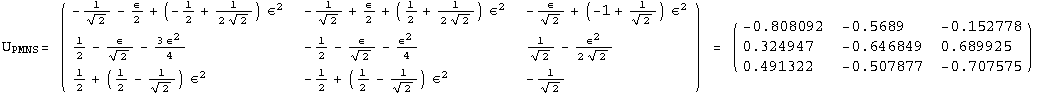
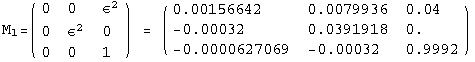
M = ( {{0, 0, ε^2}, {0, ε^2, 0}, {0, 0, 1}} ) = ( {{0.00156642, 0.0079936, 0.04}, {-0.00032, 0.0391918, 0.}, {-0.0000627069, -0.00032, 0.9992}} ) l

Chosen neutrino mass scheme: {ε^2, ε, 1}

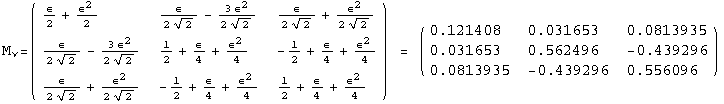
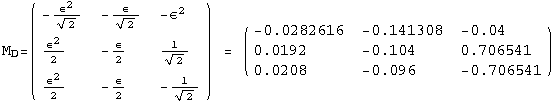
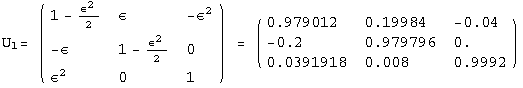
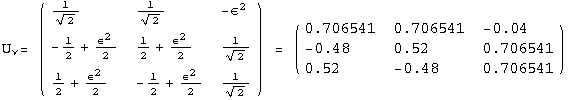
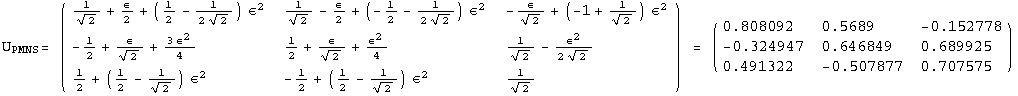
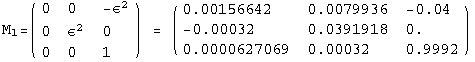
M = ( {{0, 0, -ε^2}, {0, ε^2, 0}, {0, 0, 1}} ) = ( {{0.00156642, 0.0079936, -0.04}, {-0.00032, 0.0391918, 0.}, {0.0000627069, 0.00032, 0.9992}} ) l

Chosen neutrino mass scheme: {ε^2, ε, 1}

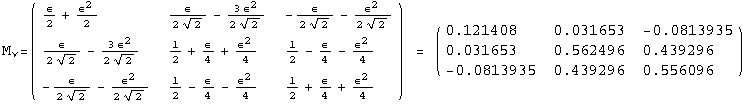
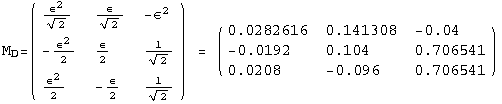
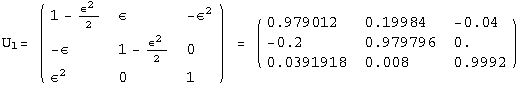
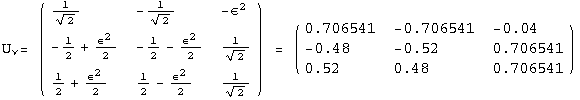
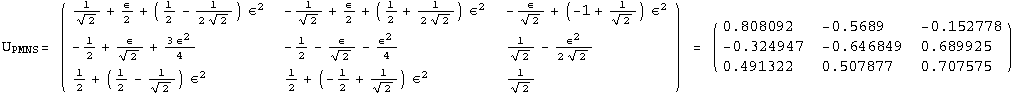
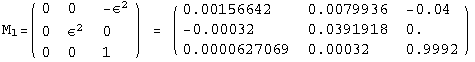
M = ( {{0, 0, -ε^2}, {0, ε^2, 0}, {0, 0, 1}} ) = ( {{0.00156642, 0.0079936, -0.04}, {-0.00032, 0.0391918, 0.}, {0.0000627069, 0.00032, 0.9992}} ) l

Chosen neutrino mass scheme: {ε^2, ε, 1}

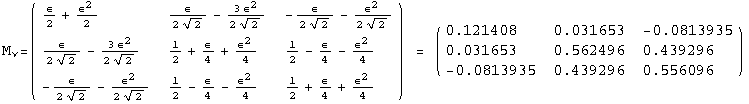
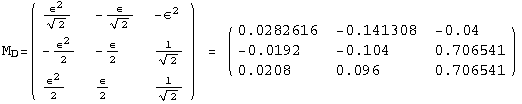
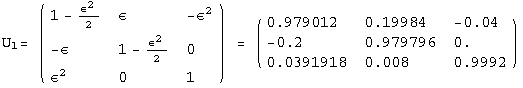
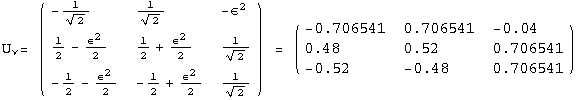
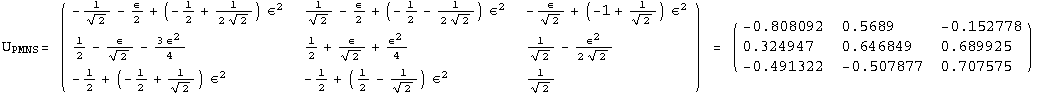
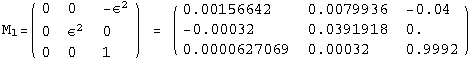
M = ( {{0, 0, -ε^2}, {0, ε^2, 0}, {0, 0, 1}} ) = ( {{0.00156642, 0.0079936, -0.04}, {-0.00032, 0.0391918, 0.}, {0.0000627069, 0.00032, 0.9992}} ) l

Chosen neutrino mass scheme: {ε^2, ε, 1}

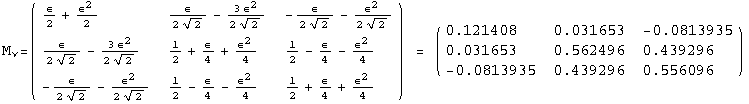
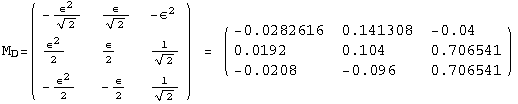
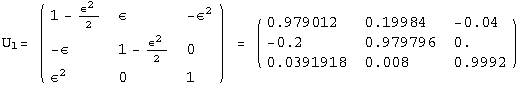
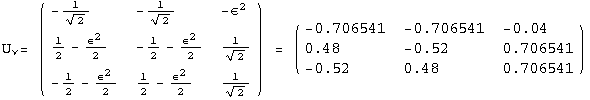
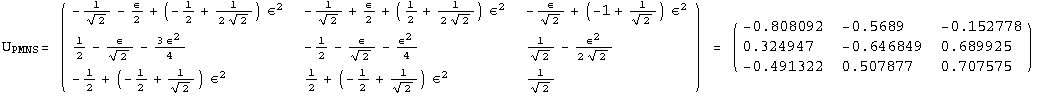
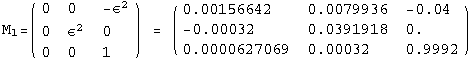
M = ( {{0, 0, -ε^2}, {0, ε^2, 0}, {0, 0, 1}} ) = ( {{0.00156642, 0.0079936, -0.04}, {-0.00032, 0.0391918, 0.}, {0.0000627069, 0.00032, 0.9992}} ) l

Chosen neutrino mass scheme: {ε^2, ε, 1}

Chosen neutrino mass scheme: {ε^2, ε, 1}

Chosen neutrino mass scheme: {ε^2, ε, 1}

Chosen neutrino mass scheme: {ε^2, ε, 1}

Chosen neutrino mass scheme: {ε^2, ε, 1}

Chosen neutrino mass scheme: {ε^2, ε, 1}

Chosen neutrino mass scheme: {ε^2, ε, 1}

Chosen neutrino mass scheme: {ε^2, ε, 1}

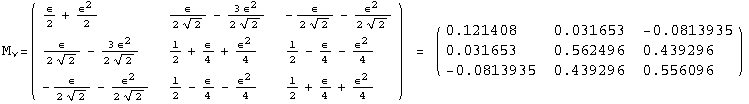
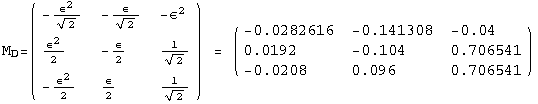
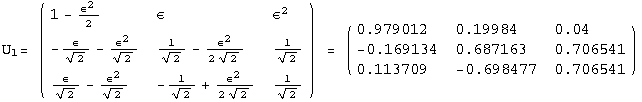
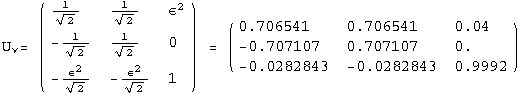
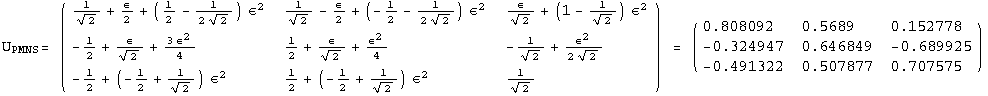
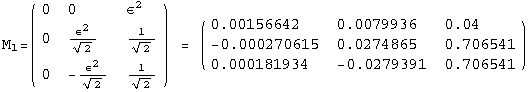
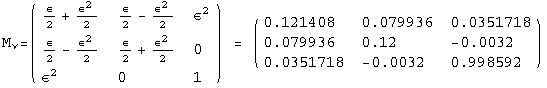
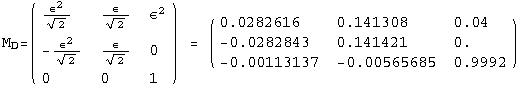
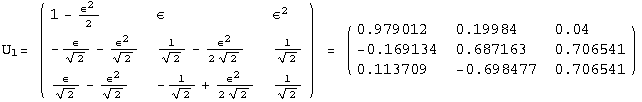
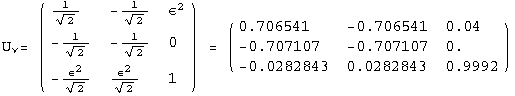
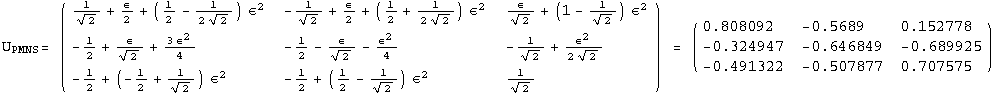
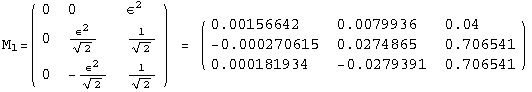
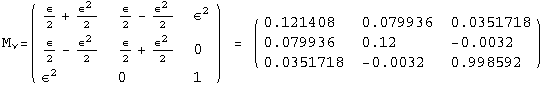
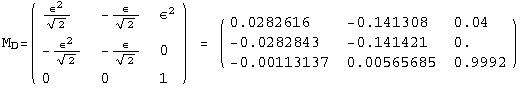
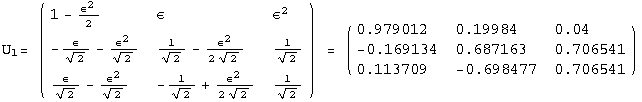
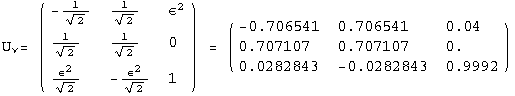
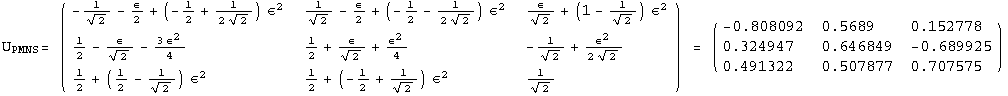
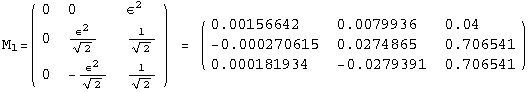
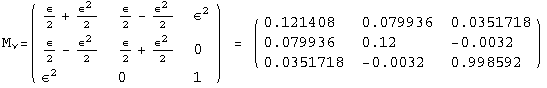
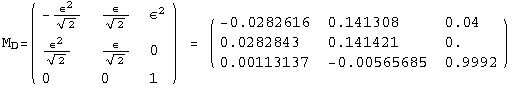
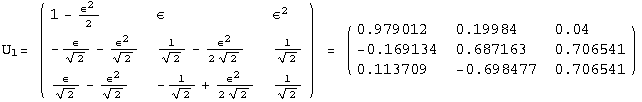
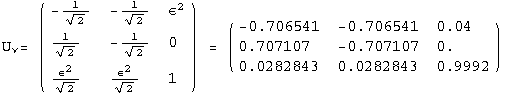
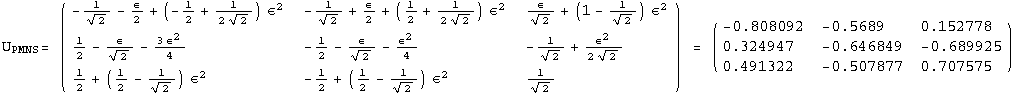
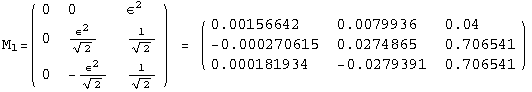
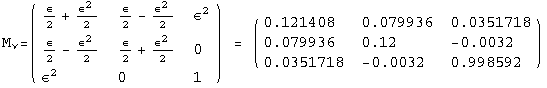
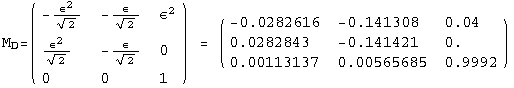
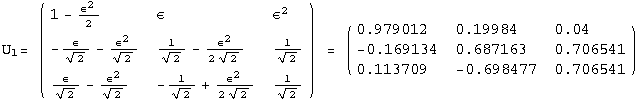
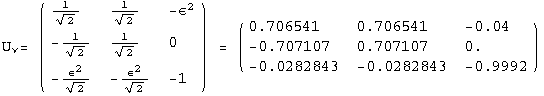
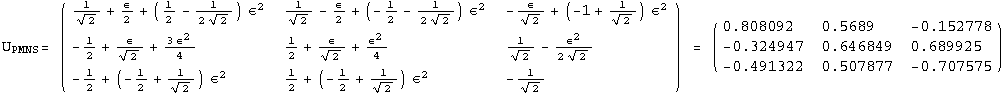
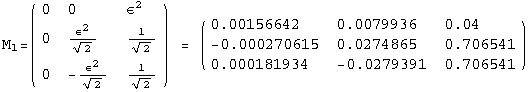
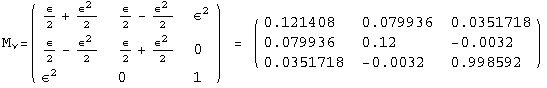
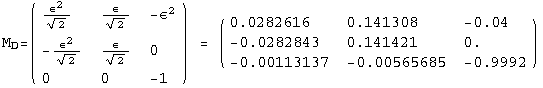
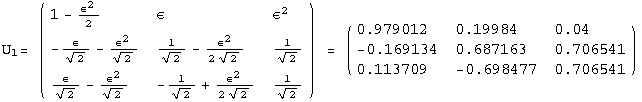
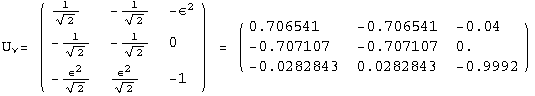
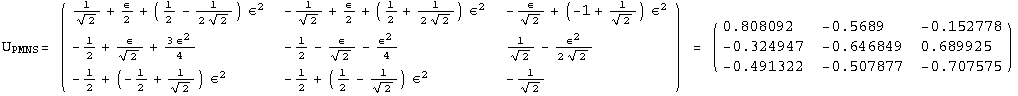
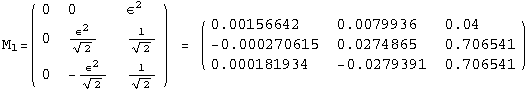
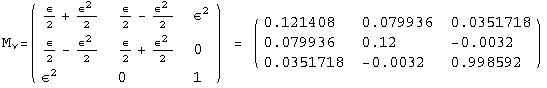
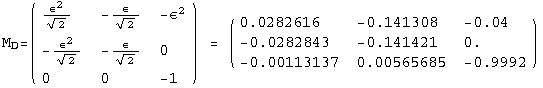
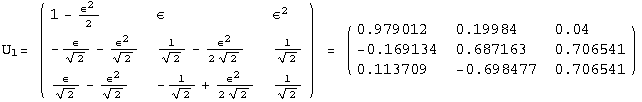
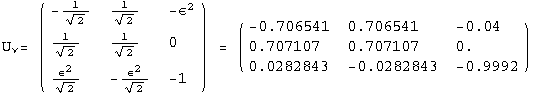
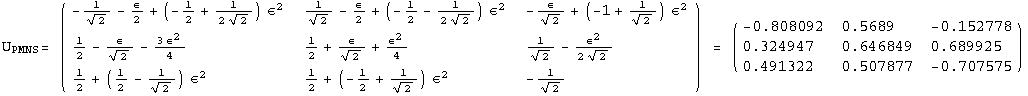
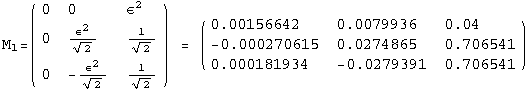
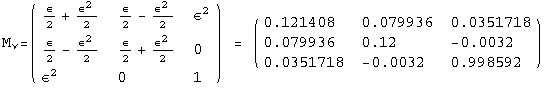
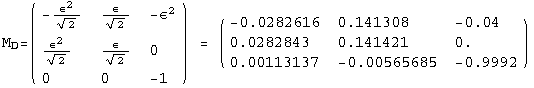
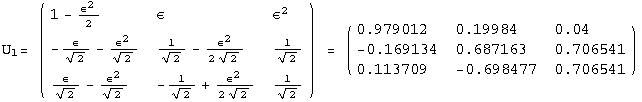
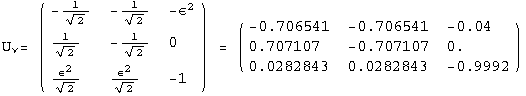
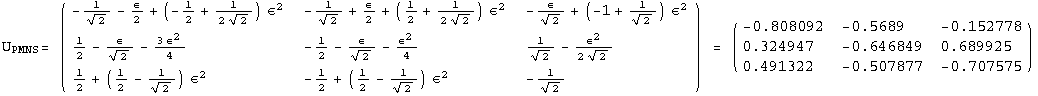
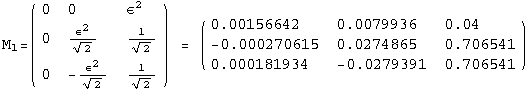
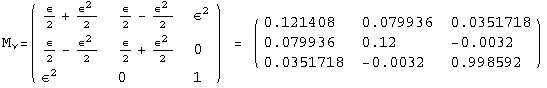
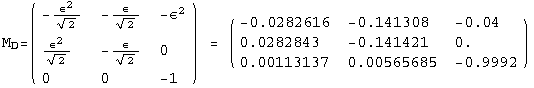
Created by Mathematica  (December 14, 2006) Valid XHTML 1.1!