The weighted event error discussion ....

---

• Errors and binning of the Cos(theta)-Plot for Nature.

  Summary:
  We argue that the error treatment given to the MC-events in the Nature-draft cos(theta) plot is wrong.

  It is also suggested to take the 2-fold bin width, to minimize the statistical fluctuations in data and MC.

  In detail:

  • An analysis of the errors given in the recent Madison Darft of the Nature Paper was done.
    See here for the original plot, as from draft-08-01-2000 .

    This analysis was motivated by
    (1) the large value of the errors (comparable to the data), and
    (2) and by their large large fluctuation from bin to bin (up to 4-5 times).
    It was felt that the conclusion from this plot could be, that the MC-signal prediction is quite uncertain (at least of low statistical significance).

  • The Madison plot was redone, using a different treatment of the errors of the MC events in each cos(theta) bin.
    We used the weighted event handling as

    variance_mean = sum( weigth_i**2), i=1,k

    where the sum goes over all k events in a given histogram bin, and weigth_i is the weight of the i-th event.

    This procedure is accepted standard (see e.g. G.Zech, DESY--95-113), and also implemented in the Hbook-library (when selected).

    This procedure is different from Ty's handling of the MC-data, as he explained recently in an email (June12th).
    He splits the sample per bin in 4 subsamples (of roughly same size), and approximates the variance of the average by the variance of the averages of the 4 subsamples.

    The resulting plot for the cos(theta)-distribution with the standard error treatment given here as ps-file.
    

    Here, we compare the original figure with the proposed in this note error treatment.
    
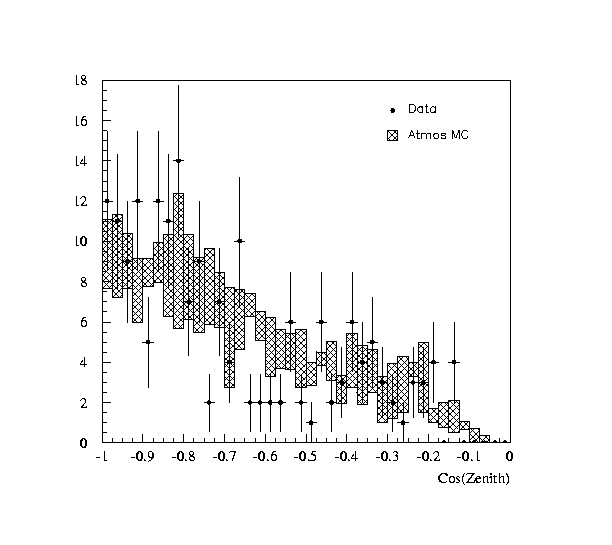
    Figure 1: Cos(Zenit) as of the Natrue draft.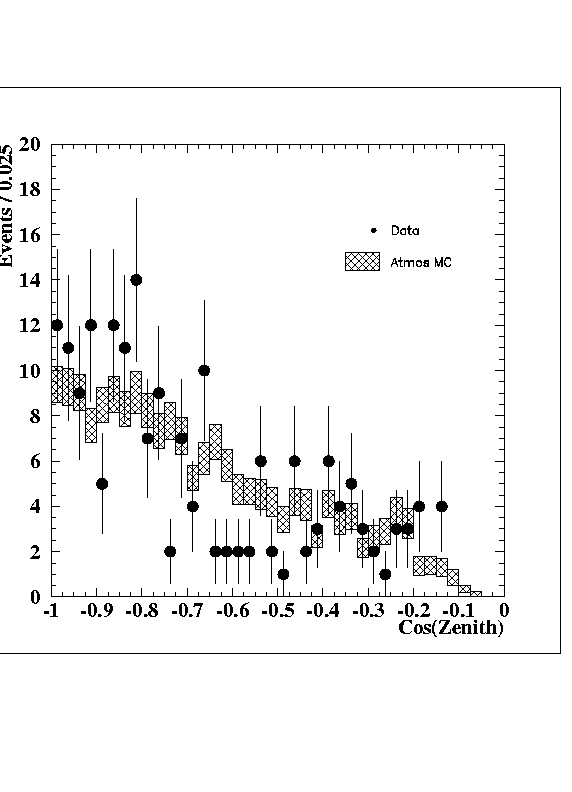
    Figure 2: Cos(Zenit) with smaller errors.

    We conclude, that the size of the MC-errors are smaller, in particular, the fluctuations of the weights in neighbouring bins is much reduced and practically uniform, as expected from the similar number of equivalent events, found in the most populated bins.
    The total number of equivalent events, to which the 7411 MC events correspond, is 2200.2 events.
    Note, that the other atmospheric Neutrino sample (Eva's files) contain the same number of 2100 events. This means, that with current sample size the weighted MC-technique has no (statistically significant) improvement.

    To compare the errors applied in both plots, see here.

    The upper plot shows the distribution of erorrs for the 40 bins in cos(theta), as described in this note.
    The lower plot is the Madison-error treatment.
    The fluctuation of the Madison errors, is larger by a factor of 3, the average value is 50% higher.

  • It is felt, that the statistical errors are large for MC and data in the current binning in cos(theta), which is 0.025.

    Here we present combined plots for 3 different binwidths.
    The 3 plots on each page are for binsize: 0.025, 0.050, 0.10 in cos(theta).
    The first set of plots uses the "rectangle error option" in PAW (e2),
    the second set of plots draws an error-band (option e3).

    For separate plots (ps-files), check here:
    for bin=0.025 , for bin=0.050 , and for bin=0.10 .

    The last 3 separate plots account for another effect, which was previously neglected:
    We calculate the error for each data point,
    using the binomial error statistics rather than poissonian.
    Note that this assumes we are using the presented data in the framework of "density (or shape) distributions", i.e. suited to compare with other distributions. (In this case the total number of entries in the histogram is assumed to be "fixed".)

    This reduces the error bars by 13% in the first 2 bins of the last plot.

    Here we give the Numbers of entries and errors for all the MC and data histograms entering the above plots.
    Suggested for Chi2/Kolmogorov/..-tests and final consistency checks (UW?).

    My suggestion is to take the binwidth=0.05 (right upper plot),
    and work on the error-band MC-presentation (i.e. avoid the sharp up/down by a more sophisticated smoothing procedure than the one presented here).

  Note in addition to the MC error handling, that for larger binwidth another correction to the data-errors has to be done, since the limitation of the poissonian approximation will be relevant. This has been done for the 3 separate plots above, as explained in the text.

  Thanks to Ty for suppling the data and MC events, and also his kumac. This made a quick degbugging of the difference in the error-treatments possible.

Return to previous page .

Author of this page:
Ralf Wischnewski
08-August-2000