 |
||||||||||||||||||||
| Abstract | ||||||||||||||||||||
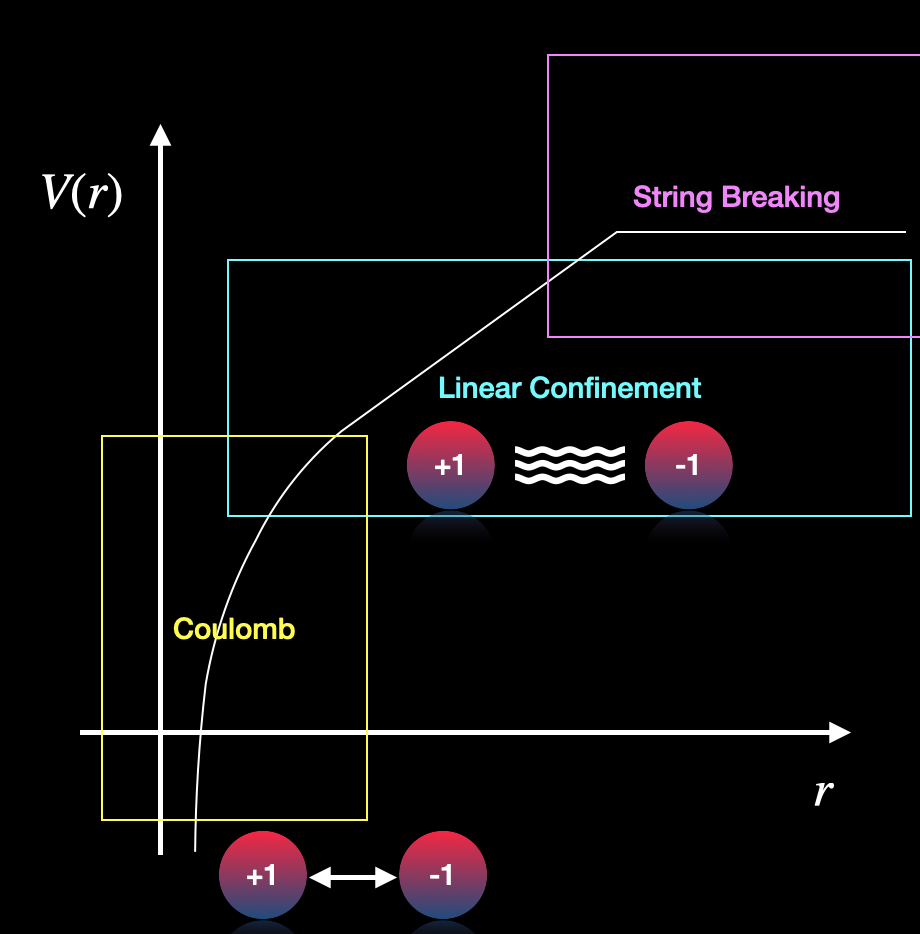
| Compact lattice Quantum Electrodynamics is a complex quantum field theory with dynamical gauge and matter fields and it has similarities with Quantum Chromodynamics, in particular asymptotic freedom and confinement. We consider a (2+1)-dimensional lattice discretization of Quantum Electrodynamics with the inclusion of dynamical fermionic matter. We define a suitable quantum algorithm to measure the static potential as a function of the distance between two charges on the lattice and we use a variational quantum calculation to explore the Coulomb, confinement and string breaking regimes. A symmetry-preserving and resource-efficient variational quantum circuit is employed to prepare the ground state of the theory at various values of the coupling constant, corresponding to different physical distances, allowing the accurate extraction of the static potential from a quantum computer. We demonstrate that results from quantum experiments on the Quantinuum H1-1 trapped-ion device and emulator, with full connectivity between qubits, agree with classical noiseless simulations using circuits with 10 and 24 qubits. Moreover, we visualize the electric field flux configurations that mostly contribute in the wave-function of the quantum ground state in the different regimes of the potential, thus giving insights into the mechanisms of confinement and string breaking. These results are a promising step forward in the grand challenge of solving higher dimensional lattice gauge theory problems with quantum computing algorithms. |
 |
|
| Abstract | |
| This paper presents a hybrid quantum-classical approach to prime factorization. The proposed algorithm is based on the Variational Quantum Eigensolver (VQE), which employs a classical optimizer to find the ground state of a given Hamiltonian. A numerical study is presented, evaluating the performance of the proposed method across various instances on both IBM's real quantum computer and its classical simulator. The results demonstrate that the method is capable of successfully factorizing numbers up to 253 on a real quantum computer and up to 1048561 on a classical simulator. These findings show the potential of the approach for practical applications on near-term quantum computers. |
| Abstract | |
| In this paper, a Hamiltonian lattice formulation for 2+1D compact Maxwell-Chern-Simons theory is derived. We analytically solve this theory and demonstrate that the mass gap in the continuum limit matches the well-known continuum formula. Our formulation preserves topological features such as the quantization of the Chern-Simons level, the degeneracy of energy eigenstates, the non-trivial properties of Wilson loops, and the mutual and self statistics of anyons. This work lays the groundwork for future Hamiltonian-based simulations of Maxwell-Chern-Simons theory on classical and quantum computers. |
| Abstract | |
| In this paper, we examine a compact U(1) lattice gauge theory in (2+1) dimensions and present a strategy for studying the running coupling and extracting the non-perturbative Λ-parameter. To this end, we combine Monte Carlo simulations and quantum computing, where the former can be used to determine the numerical value of the lattice spacing a, and the latter allows for reaching the perturbative regime at very small values of the bare coupling and, correspondingly, small values of a. The methodology involves a series of sequential steps (i.e., the step scaling function) to bridge results from small lattice spacings to non-perturbative large-scale lattice calculations. Focusing on the pure gauge case, we demonstrate that these quantum circuits, adapted to gauge degrees of freedom, are able to capture the relevant physics by studying the expectation value of the plaquette operator, for matching with corresponding Monte Carlo simulations. We also present results for the static potential and static force, which can be related to the renormalized coupling. The procedure outlined in this work can be extended to Abelian and non-Abelian lattice gauge theories with matter fields and might provide a way towards studying lattice quantum chromodynamics utilizing both quantum and classical methods. |
| Abstract | |
| Geometric quantum machine learning based on equivariant quantum neural networks (EQNN) recently appeared as a promising direction in quantum machine learning. Despite the encouraging progress, the studies are still limited to theory, and the role of hardware noise in EQNN training has never been explored. This work studies the behavior of EQNN models in the presence of noise. We show that certain EQNN models can preserve equivariance under Pauli channels, while this is not possible under the amplitude damping channel. We claim that the symmetry breaking grows linearly in the number of layers and noise strength. We support our claims with numerical data from simulations as well as hardware up to 64 qubits. Furthermore, we provide strategies to enhance the symmetry protection of EQNN models in the presence of noise. |
| Abstract | |
| We explore the first-order phase transition in the lattice Schwinger model in the presence of a topological theta-term by means of the variational quantum eigensolver (VQE). Using two different fermion discretizations, Wilson and staggered fermions, we develop parametric ansatz circuits suitable for both discretizations, and compare their performance by simulating classically an ideal VQE optimization in the absence of noise. The states obtained by the classical simulation are then prepared on the IBM's superconducting quantum hardware. Applying state-of-the art error-mitigation methods, we show that the electric field density and particle number, observables which reveal the phase structure of the model, can be reliably obtained from the quantum hardware. To investigate the minimum system sizes required for a continuum extrapolation, we study the continuum limit using matrix product states, and compare our results to continuum mass perturbation theory. We demonstrate that taking the additive mass renormalization into account is vital for enhancing the precision that can be obtained with smaller system sizes. Furthermore, for the observables we investigate we observe universality, and both fermion discretizations produce the same continuum limit. |
| Abstract | |
| Quantum computing provides a novel avenue towards simulating dynamical phe- nomena, and, in particular, scattering pro- cesses relevant for exploring the struc- ture of matter. However, preparing and evolving particle wave packets on a quan- tum device is a nontrivial task. In this work, we propose a method to prepare Gaussian wave packets with momentum on top of the interacting ground state of a fermionic Hamiltonian. Using Givens ro- tation, we show how to efficiently obtain expectation values of observables through- out the evolution of the wave packets on digital quantum computers. We demon- strate our technique by applying it to the staggered lattice formulation of the Thirring model and studying the scatter- ing of two wave packets. Monitoring the particle density and the entropy produced during the scattering process, we char- acterize the phenomenon and provide a first step towards studying more compli- cated collision processes on digital quan- tum computers. In addition, we perform a small-scale demonstration on IBM’s quan- tum hardware, showing that our method is suitable for current and near-term quan- tum devices. |
| Abstract | |
| We study the flight gate assignment problem on IonQ's Aria trapped ion quantum computer using the variational quantum eigensolver. Utilizing the conditional value at risk as an aggregation function, we demonstrate that current trapped ion quantum hardware is able to obtain good solutions for this combinatorial optimization problem with high probability. In particular, we run the full variational quantum eigensolver for small instances and we perform inference runs for larger systems, demonstrating that current and near-future quantum hardware is suitable for addressing combinatorial optimization problems. |
| Abstract | |
| Operator controllability refers to the ability to implement an arbitrary unitary in SU(N) and is a prerequisite for universal quantum computing. Controllability tests can be used in the design of quantum devices to reduce the number of external controls. Their practical use is hampered, however, by the exponential scaling of their numerical effort with the number of qubits. Here, we devise a hybrid quantum-classical algorithm based on a parametrized quantum circuit. We show that controllability is linked to the number of independent parameters, which can be obtained by dimensional expressivity analysis. We exemplify the application of the algorithm to qubit arrays with nearest-neighbour couplings and local controls. Our work provides a systematic approach to the resource-efficient design of quantum chips. |
| Abstract | ||||||||||||||||||||
| We propose an ansatz quantum circuit for the variational quantum eigensolver (VQE), suitable for exploring the phase structure of the multi-flavor Schwinger model in the presence of a chemical potential. Our ansatz is capable of incorporating relevant model symmetries via constrains on the parameters, and can be implemented on circuit-based as well as measurement-based quantum devices. We show via classical simulation of the VQE that our ansatz is able to capture the phase structure of the model, and can approximate the ground state to a high level of accuracy. Moreover, we perform proof-of-principle simulations on superconducting, gate-based quantum hardware. Our results show that our approach is suitable for current gate-based quantum devices, and can be readily implemented on measurement-based quantum devices once available. |
| Abstract | |
| Gauge theories establish the standard model of particle physics, and lattice gauge theory (LGT) calculations employing Markov Chain Monte Carlo (MCMC) methods have been pivotal in our understanding of fundamental interactions. The present limitations of MCMC techniques may be overcome by Hamiltonian-based simulations on classical or quantum devices, which further provide the potential to address questions that lay beyond the capabilities of the current approaches. However, for continuous gauge groups, Hamiltonian-based formulations involve infinite-dimensional gauge degrees of freedom that can solely be handled by truncation. Current truncation schemes require dramatically increasing computational resources at small values of the bare couplings, where magnetic field effects become important. Such limitation precludes one from `taking the continuous limit' while working with finite resources. To overcome this limitation, we provide a resource-efficient protocol to simulate LGTs with continuous gauge groups in the Hamiltonian formulation. Our new method allows for calculations at arbitrary values of the bare coupling and lattice spacing. The approach consists of the combination of a Hilbert space truncation with a regularization of the gauge group, which permits an efficient description of the magnetically-dominated regime. We focus here on Abelian gauge theories and use 2+1 dimensional quantum electrodynamics as a benchmark example to demonstrate this efficient framework to achieve the continuum limit in LGTs. This possibility is a key requirement to make quantitative predictions at the field theory level and offers the long-term perspective to utilise quantum simulations to compute physically meaningful quantities in regimes that are precluded to quantum Monte Carlo. |
| Abstract | |
| We propose to utilize NISQ-era quantum devices to compute short distance quantities in (2+1)-dimensional QED and to combine them with large volume Monte Carlo simulations and perturbation theory. On the quantum computing side, we perform a calculation of the mass gap in the small and intermediate regime, demonstrating, in the latter case, that it can be resolved reliably. The so obtained mass gap can be used to match corresponding results from Monte Carlo simulations, which can be used eventually to set the physical scale. In this paper we provide the setup for the quantum computation and show results for the mass gap and the plaquette expectation value. In addition, we discuss some ideas that can be applied to the computation of the running coupling. Since the theory is asymptotically free, it would serve as a training ground for future studies of QCD in (3+1)-dimensions on quantum computers. |
| Abstract | |
| Variational quantum eigensolvers (VQEs) combine classical optimization with efficient cost function evaluations on quantum computers. We propose a new approach to VQEs using the principles of measurement-based quantum computation. This strategy uses entagled resource states and local measurements. We present two measurement-based VQE schemes. The first introduces a new approach for constructing variational families. The second provides a translation of circuit-based to measurement-based schemes. Both schemes offer problem-specific advantages in terms of the required resources and coherence times. |
| Abstract | |
| It has recently been shown that vacuum expectation values and Feynman path integrals can be regularized using Fourier integral operator ζ-function, yet the physical meaning of these ζ-regularized objects was unknown. Here we show that ζ-regularized vacuum expectations appear as continuum limits using a certain discretization scheme. Furthermore, we study the rate of convergence for the discretization scheme using the example of a one-dimensional hydrogen atom in (-π,π) which we evaluate classically, using the Rigetti Quantum Virtual Machine, and on the Rigetti 8Q quantum chip Agave device. We also provide the free radiation field as an example for the computation of ζ-regularized vacuum expectation values in a gauge theory. |
 |
|
| Abstract | |
| Lattice gauge theories, which originated from particle physics in the context of Quantum Chromodynamics (QCD), provide an important intellectual stimulus to further develop quantum information technologies. While one long-term goal is the reliable quantum simulation of currently intractable aspects of QCD itself, lattice gauge theories also play an important role in condensed matter physics and in quantum information science. In this way, lattice gauge theories provide both motivation and a framework for interdisciplinary research towards the development of special purpose digital and analog quantum simulators, and ultimately of scalable universal quantum computers. In this manuscript, recent results and new tools from a quantum science approach to study lattice gauge theories are reviewed. Two new complementary approaches are discussed: first, tensor network methods are presented - a classical simulation approach - applied to the study of lattice gauge theories together with some results on Abelian and non-Abelian lattice gauge theories. Then, recent proposals for the implementation of lattice gauge theory quantum simulators in different quantum hardware are reported, e.g., trapped ions, Rydberg atoms, and superconducting circuits. Finally, the first proof-of-principle trapped ions experimental quantum simulations of the Schwinger model are reviewed. |