| Abstract |
| We propose a quantum error mitigation scheme for single-qubit measurement errors, particularly suited for one-way quantum computation. Contrary to well established error mitigation methods for circuit-based quantum computation, that require to run the circuits several times, our method is capable of mitigating measurement errors in real-time, during the processing measurements of the one-way computation. For that, an ancillary qubit register is entangled with the to-be-measured qubit and additionally measured afterwards. By using a voting protocol on all measurement outcomes, occurring measurement errors can be mitigated in real-time while the one-way computation continues. We provide an analytical expression for the probability to detect a measurement error in dependency of the error rate and the number of ancilla qubits. From this, we derive an estimate of the ancilla register size for a given measurement error rate and a required success probability to detect a measurement error. Additionally, we also consider the CNOT gate error in our mitigation method and investigate how this influences the probability to detect a measurement error. Finally, we show in proof-of-principle simulations, also considering a hardware noise model, that our method is capable of reducing the measurement errors significantly in a one-way quantum computation with only a small number of ancilla qubits. |
| Abstract | |
| We review two algorithmic advances that bring us closer to reliable quantum simulations of model systems in high energy physics and beyond on noisy intermediate-scale quantum (NISQ) devices. The first method is the dimensional expressivity analysis of quantum circuits, which allows for constructing minimal but maximally expressive quantum circuits. The second method is an efficient mitigation of readout errors on quantum devices. Both methods can lead to significant improvements in quantum simulations, e.g., when variational quantum eigensolvers are used. |
| Abstract | |
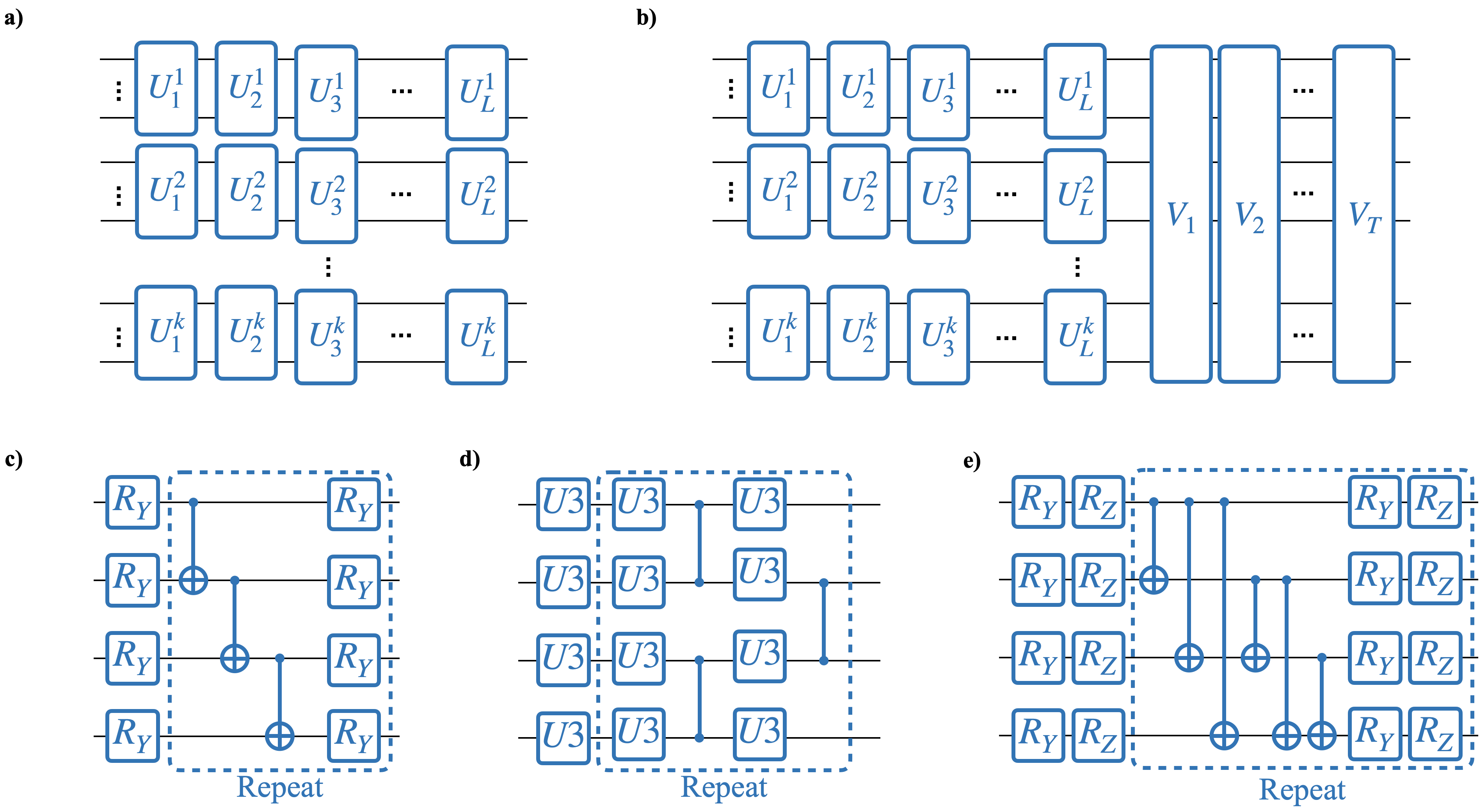
| Parametric quantum circuits play a crucial role in the performance of many variational quantum algorithms. To successfully implement such algorithms, one must design efficient quantum circuits that sufficiently approximate the solution space while maintaining a low parameter count and circuit depth. In this paper, we develop a method to analyze the dimensional expressivity of parametric quantum circuits. Our technique allows for identifying superfluous parameters in the circuit layout and for obtaining a maximally expressive ansatz with a minimum number of parameters. Using a hybrid quantum-classical approach, we show how to efficiently implement the expressivity analysis using quantum hardware, and we provide a proof of principle demonstration of this procedure on IBM's quantum hardware. We also discuss the effect of symmetries and demonstrate how to incorporate or remove symmetries from the parametrized ansatz. |
| Abstract | |
| Variational quantum eigensolvers (VQEs) combine classical optimization with efficient cost function evaluations on quantum computers. We propose a new approach to VQEs using the principles of measurement-based quantum computation. This strategy uses entagled resource states and local measurements. We present two measurement-based VQE schemes. The first introduces a new approach for constructing variational families. The second provides a translation of circuit-based to measurement-based schemes. Both schemes offer problem-specific advantages in terms of the required resources and coherence times. |
| Abstract | |
| Quantum technologies offer the prospect to efficiently simulate sign-problem afflicted regimes in lattice field theory, such as the presence of topological terms, chemical potentials, and out-of-equilibrium dynamics. In this work, we derive the (3+1)D topological θ-term for Abelian and non-Abelian lattice gauge theories in the Hamiltonian formulation, paving the way towards Hamiltonian-based simulations of such terms on quantum and classical computers. We further study numerically the zero-temperature phase structure of a (3+1)D U(1) lattice gauge theory with the θ-term via exact diagonalization for a single periodic cube. In the strong coupling regime, our results suggest the occurrence of a phase transition at constant values of θ, as indicated by an avoided level-crossing and abrupt changes in the plaquette expectation value, the electric energy density, and the topological charge density. These results could in principle be cross-checked by the recently developed (3+1)D tensor network methods and quantum simulations, once sufficient resources become available. |
 |
|
| Abstract | |
| Barren plateaus appear to be a major obstacle to using variational quantum algorithms to simulate large-scale quantum systems or replace traditional machine learning algorithms. They can be caused by multiple factors such as expressivity, entanglement, locality of observables, or even hardware noise. We propose classical splitting of ansätze or parametrized quantum circuits to avoid barren plateaus. Classical splitting is realized by splitting an N qubit ansatz to multiple ansätze that consists of O(log N) qubits. We show that such an ansatz can be used to avoid barren plateaus. We support our results with numerical experiments and perform binary classification on classical and quantum datasets. Then, we propose an extension of the ansatz that is compatible with variational quantum simulations. Finally, we discuss a speed-up for gradient-based optimization and hardware implementation, robustness against noise and parallelization, making classical splitting an ideal tool for noisy intermediate scale quantum (NISQ) applications. |
| Abstract | |
| We present a variational quantum eigensolver (VQE) algorithm for the efficient bootstrapping of the causal representation of multiloop Feynman diagrams in the Loop-Tree Duality (LTD) or, equivalently, the selection of acyclic configurations in directed graphs. A loop Hamiltonian based on the adjacency matrix describing a multiloop topology, and whose different energy levels correspond to the number of cycles, is minimized by VQE to identify the causal or acyclic configurations. The algorithm has been adapted to select multiple degenerated minima and thus achieves higher detection rates. A performance comparison with a Grover's based algorithm is discussed in detail. The VQE approach requires, in general, fewer qubits and shorter circuits for its implementation, albeit with lesser success rates. |