-
"Virtual Hadronic and Heavy-Fermion O(alpha**2) Corrections to Bhabha Scattering"
S. Actis, M. Czakon, J. Gluza, T. Riemann
arXiv:0807.4691, DESY-08-101, PITHA-08-18, submitted to Phys. Rev. D
NNLO loop corrections from massive flavors and from hadrons to Bhabha scattering in the limit of fixed angle and high energy for Meson Factories, LEP, ILC
Long write-up of material presented in Phys.Rev.Lett. 100 (2008) 131602
Application of dispersion technique to the Bhabha two-loop box diagrams
Comprehensive collection of different two-loop contributions with heavy fermions/hadrons
Numerics for leptons and hadrons, the latter based on H. Burkhardt's parameterization repi.f of R_had
Auxiliary files:
DispersionBoxKernelMasters.m: The eight master integrals MA1 (B1) to MA8 (B8) [typo of eq.-numbering in arXiv:0807.4691], and the box kernel functions KA[s,t,z], KB[s,t,z], KC[s,t,z] expressed by them as exact functions of \epsilon, s, t, m (=m_e), z (=m_heavy^2); the expressions KAexp[s_,t_,z_], KBexp[s_,t_,z_], KCexp[s_,t_,z_] are the kernels KA, KB, KC of eqs.(71)-(73), where m_e^2 << s,t,u,z is assumed; the expressions BA, BB, BC are the analytically integrated box functions (for fermions, with R_had replaced by R_f) as published in eq.(3.20) to eq.(3.22) of Nucl.Phys. B786 (2007) 26-51; the threshold function R[u] (=R_f(u) of eq.(23) with slightly changed normalization) for fermions including the order \epsilon
KernelFunctions.m: Self-energy kernel eq.(30), vertex kernel eq.(43), and three box kernels KA, KB, KC of eqs.(71)-(73); they are used for the corresponding folding in the dispersion integrals over R_had
BoxFunctions.m: The three resulting box kernels I1 eq.(75) and I2 eq.(76) for the Bhabha cross-section formula after summing over all box diagrams
Integrands.m: The infrared safe kernel functions F1 to F4, eqs. (88)-(91) for the Bhabha cross-section, covering box diagrams and IR-non-safe diagrams
repi_1986.f: The parameterization of H. Burkhardt (1986) for R_had(s) as described in Appendix E and used for the numerics of Table III and Table IV and in Figures 9-14, 16 (called there "parameterization hadronic 1")
repi_2.f: The parameterization for R_had(s) as described in items (A) to (C) in Appendix E, used for the numerics in Figures 9, 11, and 15, 16 (called there "parameterization hadronic 2")
cpolylog.f: Fortran code for the evalution of complex polylogarithmic functions Li_2(z) and Li_3(z) as described in Appendix F, assuming a cut at the positive real axis starting at z=1
bhbhnnlohf: Fortran package for the evalution of the Bhabha cross section contributions from all the described contributions, see article for details. -
"Virtual Hadronic and Leptonic Contributions to Bhabha Scattering"
S. Actis, M. Czakon, J. Gluza, T. Riemann
arXiv:0711.3847, Phys.Rev.Lett. 100 (2008) 131602
NNLO loop corrections from massive flavors and from hadrons to Bhabha scattering in the limit of fixed angle and high energy for Meson Factories, LEP, ILC
Application of dispersion technique to the Bhabha two-loop box diagrams
Numerics for leptons and hadrons, the latter based on H. Burkhardt's parameterization repi.f of R_had
For auxiliary files see KernelFunctions.m, BoxFunctions.m, Integrands.m, repi_1986.f, -
"Fermionic NNLO contributions to Bhabha scattering"
S. Actis, M. Czakon, J. Gluza, T. Riemann
arXiv:0710.5111, Acta Phys.Polon. B38 (2007) 3517-3528
Talk given at 31st International Conference of Theoretical Physics "Matter to the Deepest: Recent Development in Physics of Fundamental Interactions", Ustron, Katowice, Poland, 5-11 Sep 2007
Transparencies of the talk: ustron07-riemann.pdf
The two-loop contributions with massive flavors to Bhabha scattering in the limit of fixed angle, high energy, and arbitrary heavy fermion mass
First application of dispersion technique to the Bhabha two-loop box diagrams
Numerics for leptons -
" Two-Loop Fermionic Corrections to Massive Bhabha Scattering"
S. Actis, M. Czakon, J. Gluza, T. Riemann
arXiv:0704.2400, Nucl.Phys. B786 (2007) 26-51
The two-loop contributions with two massive flavors to Bhabha scattering in the limit of fixed angle, high energy, and intermediate heavy fermion mass
For auxiliary files see CrossSection.m, ExactResults.m, ApproxResults.m, MIs.m, -
" Planar two-loop master integrals for massive Bhabha scattering: N(f)=1 and N(f)=2"
S. Actis, M. Czakon, J. Gluza, T. Riemann
hep-ph/0609051, in: Proceedings of Loops and Legs 2006, Nucl. Phys. Proc. Suppl. 160 (2006) 91-100
The master integrals are determined for the two-loop contributions with two massive flavors to Bhabha scattering in the limit of fixed angle and high energy
For auxiliary files see later, here -
"The planar four-point master integrals for massive two-loop Bhabha scattering"
M. Czakon, J. Gluza, T. Riemann
Nucl.Phys. B751 (2006) 1-17 hep-ph/0604101
The complete set of planar four-point Master Integrals needed for massive Bhabha scattering in the limit of fixed angle and high energy at the two-loop level.
For auxiliary files see here -
"Master integrals for massive two-loop Bhabha scattering in QED"
M. Czakon, J. Gluza, T. Riemann
Phys. Rev. D71 (2005) 073009, hep-ph/0412164
Complete lists of master integrals for Bhabha scattering with one flavor (electrons) and several flavors (e.g. electrons, muons, tauons) are given and the status of the analytical evaluation is reviewed
For auxiliary files see here -
LL08, "DESY Zeuthen Workshop "Loops and Legs in Quantum Field Theory", Sondershausen, Germany, April 20-25, 2008
talk by J. Gluza, "Two-loop Bhabha scattering with Nf=2" [.pdf], E-print: arXiv:0710.5111, to appear in Nucl. Phys. B (Proc. Suppl.), DESY-08-084, PITHA-08-14 -
LCWS 2007, "International Linear Collider Workshop (LCWS07 and ILC07)", 30 May - 3 Jun 2007, Hamburg, Germany
"Two-loop heavy fermion corrections to Bhabha scattering"
S. Actis, M. Czakon, J. Gluza, T. Riemann, published in SLAC eConf C0705302, slides of PSN=TeV02, see also here for slides; DESY-07-192, LCWS-2007-TEV02,

-
Radcor 2005, "7th International Symposium on Radiative Corrections - Application of Quantum Field Theory to Phenomenology", Shonan Village, Japan, October 2-7, 2005
"Massive two-loop Bhabha scattering"
M. Czakon, J. Gluza, T. Riemann, transparencies [.ps], to appear in the proceedings -
Matter To The Deepest, "XXIX International Conference of Theoretical Physics", 8-14 September 2005, Ustron, Poland
"On master integrals for massive Bhabha scattering"
M. Czakon, J. Gluza, T. Riemann, transparencies [.ps], to appear in the proceedings in Acta Phys. Polonica -
ACAT05, "X Int. Workshop on Advanced Computing and Analysis Techniques in Physics Research", 22-27 May 2005, Zeuthen, Germany
"Harmonic polylogarithms for massive Bhabha scattering"
M. Czakon, J. Gluza, T. Riemann, hep-ph/0508212 [.ps], to appear in Nucl. Instr. Meth. A
For auxiliary files see here Workshop on Bhabha Scattering, Univ. Karlsruhe, April 21./22., 2005
talk by T. Riemann, "Master integrals for massive 2-loop Bhabha scattering" [.ps]
-
LL04, "DESY Zeuthen Workshop "Loops and Legs in Quantum Field Theory", Zinnowitz, Germany, 25-30 April 2004,
talk by J. Gluza, "Contributions to the 2-loop Bhabha process: new results" [.pdf]
The contribution to the proceedings by M. Czakon, J. Gluza, T. Riemann, "A complete set of scalar master integrals for massive 2-loop Bhabha scattering: where we are", hep-ph/0406203 [.ps], Nucl. Phys. B (Proc. Suppl.) B135 (204) 83, contains a short presentation of our approach in the 2-loop project. -
LCWS04, "International Conference on Linear Colliders", 19-23 April 2004, Paris, France
Born approximation
-
1-loop order
-
2-loop order
2-loop order: set 1/8, set 2/8, set 3/8, set 4/8, set 5/8, set 6/8, set 7/8, set 8/8
2-loop order, 1PI diagrams only self energies: 4 diagrams, 6 master integrals
vertices: 5 diagrams, 19 master integrals
boxes: 6 diagrams, 33 master integrals
1-loop: 6 master integrals of different type
SE3lx,SE5lx: A complete set of six 2-loop self energy master integrals, which is sufficient to calculate all the 2-loop Feynman diagrams
V6l4mx: The three 2-loop vertex MIs with six internal lines
V5l2mx,V5l3mx: The six 2-loop vertex MIs with five internal lines
V4l1mx...V4l4mx: The ten 2-loop vertex MIs with four internal lines
B7l4mx: The nine 2-loop box MIs with seven internal lines
B6l3mx: The ten 2-loop box MIs with six internal lines
B5l2mx: Eight of the forteen 2-loop box MIs with five internal lines
B5l3mx,B5l4mx: Six of the forteen 2-loop box MIs with five internal lines
2LSE: list of tadpole and self energy master integrals needed for each of the 2-loop self energy diagrams
2LVB: list of tadpole, self energy and vertex master integrals needed for each of the 2-loop vertex and box diagrams in a model with flavor number Nf=1.
V4 and B5 (and the corresponding masters) have also to be determined for Nf>1 cases.2LB: list of box master integrals needed for each of the 2-loop box diagrams.
SE3l1m, SE3l2mN, V4l3md, V4l4m, V4l4mN, V6l4m1, B4l2m, B5l4m, B5l4mN
M. Czakon, J. Gluza and T. Riemann, hep-ph/0406203 v2, Contrib. to the Proceedings of the Workshop ``Loops and Legs in Quantum Field Theory'', April 25-30, 2004, Zinnowitz, Germany, to appear in Nucl. Phys. (Proc. Suppl.) B135 (204) 83.
R. Bonciani, P. Mastrolia and E. Remiddi, Nucl. Phys. B690 (2004) 138, hep-ph/0311145 v2 (20 April 2004).
R. Bonciani, P. Mastrolia and E. Remiddi, Nucl. Phys. B661 (2003) 289, hep-ph/0301170 v4 (25 June 2004).
M. Argeri, P. Mastrolia and E. Remiddi, Nucl. Phys. B631 (2002) 388, hep-ph/0202123.
J. Fleischer, A.V. Kotikov and O.L. Veretin, Nucl. Phys. B547 (1999) 343, hep-ph/9808242.
A.I. Davydychev and M.Y. Kalmykov, (2003), hep-th/0303162.
V.A. Smirnov, Phys. Lett. B524 (2002) 129, hep-ph/0111160.
G. Heinrich and V.A. Smirnov, (2004), hep-ph/0406053.
R. Bonciani et al., Nucl. Phys. B681 (2004) 261, hep-ph/0310333 v3 (25 June 2004).
J. Fleischer and M. Kalmykov, Comput. Phys. Commun. 128 (2000) 531, hep-ph/9907431.
T. Binoth and G. Heinrich, Nucl. Phys. B585 (2000) 741, hep-ph/0004013.
T. Binoth and G. Heinrich, Nucl. Phys. B680 (2004) 375, hep-ph/0305234.
MastersBhabha.m: A mathematica file with master integrals (so far not updated compared to hep-ph/0406203 by the additional masters given in hep-ph/0412164)
Substitutions_V5l2m2.m: Some algebraic substitutions for the evaluation of scalar integrals of prototype V5l2m2 in terms of master integrals, which have been used in hep-ph/0412164, but are not given explicitely there.
HPL4.m: A mathematica file with Harmonic Polylogarithms up to weight 4
The status of the project has been described on several occasions:
The Feynman Diagrams
The virtual QED corrections
are due to the following collection of Feynman diagrams in
To be definite, we assume three generations of leptons. Further, we do not show the Feynman diagrams for the renormalization of external legs.
The Master Integrals
Such a calculation contains
several key elements. The corrections may be written in terms of some
set of scalar integrals, which are then subject of reliable
analytical and/or numerical evaluation. A non-trivial problem is the
determination of a sufficiently small, but complete set of scalar
integrals, the so-called master integrals.
There are only few
different topologies of diagrams to be calculated, they include
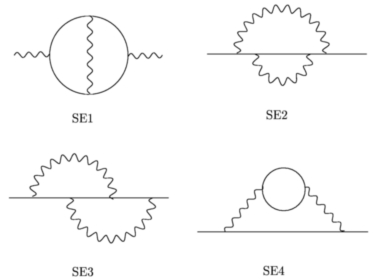
Self-energies
There are contributions from
four 2-loop self-energies.
Diagram SE1 is needed for the
evaluation of the Bhabha cross section, and SE2 to SE4 are needed for
the renormalization of external fermion legs:
Vertices
There are contributions from five 2-loop vertices:
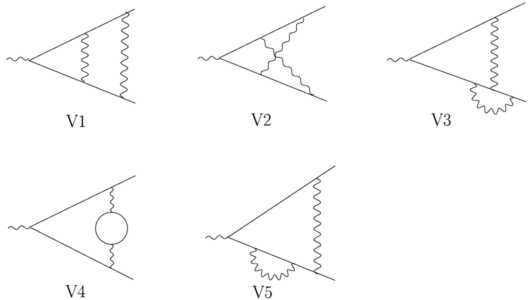
A complete set of nineteen
2-loop vertex master integrals, which is sufficient to calculate
all the vertex and box Feynman diagrams:
Boxes
There are contributions from six 2-loop boxes:
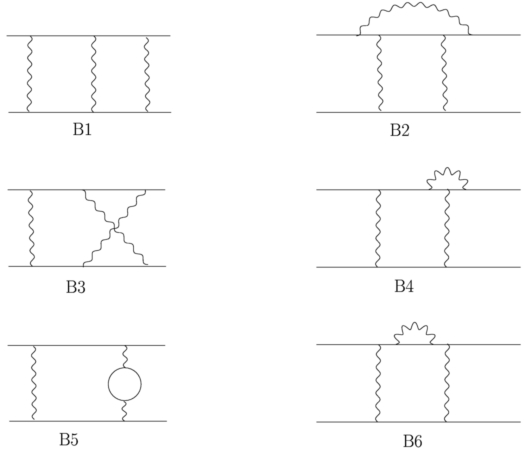
A complete set of thirty
three 2-loop box master integrals, which is sufficient to
calculate all the box Feynman diagrams:
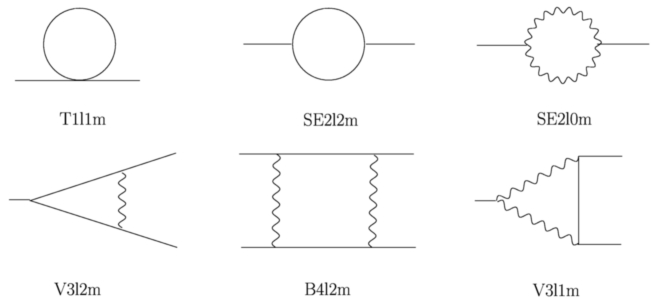
1-loop masters
There are six 1-loop master integrals needed for the evaluation of the 2-loop diagrams:
Who needs whom?
For the calculation of a
certain diagram out of the set of diagrams
[SE1,..Se4,V1,..V5,B1,..B6] only a certain subset of master integrals
will be needed.
In the following table, we indicate the number of
(2-loop + 1-loop) master integrals needed to calculate the 2-loop
vertex diagrams V1 to V5 and box diagrams B1 to B6:
In the next three tables, a '+'
means that the corresponding master integral contributes to the
diagram.
Stars denote 1-loop MIs, and the terminus 'oms' means
on-mass-shell.
For the 2-loop master integrals, we indicate also
the reference if the master is known analytically (status of June
2004).
Explicit analytical expressions for master integrals
The file
contains the analytical
expressions for all the self energy and vertex master integrals
needed, and also for few of the box master integrals, which we
calculated so far.
The analytical expressions are numerically
checked using sector decomposition as proposed in [11,12].
The
master integrals are identified with the names of the masters as
given in the figures accessible above on this page.
Comparisons
Our set of master integrals
includes also masters which were calculated earlier by other groups.
For references we refer to the tables given above: 2LSE,
2LVB, 2LB.
In comparisons, one has to take into account the different
normalizations of the master integrals as well as the different
definitions of their series expansions in (d-4).
For some time there was a disagreement of the following master integrals in MastersBhabha.m with expressions published earlier (see also hep-ph/0406203 [.ps]):
More details: see here.
For the references [3] and [9] Errata have been prepared by the authors and
FORM files with analytical expressions with the master integrals
of
[3]
and of
[9]
habe been made available at the
Bhabha
scattering web pages at Freiburg University.
References
The following articles have been quoted in this webpage and in the tables:
Additional information related to hep-ph/0412164:
In M. Czakon, J. Gluza, T. Riemann, "Master integrals for massive two-loop Bhabha scattering in QED" we refer to: